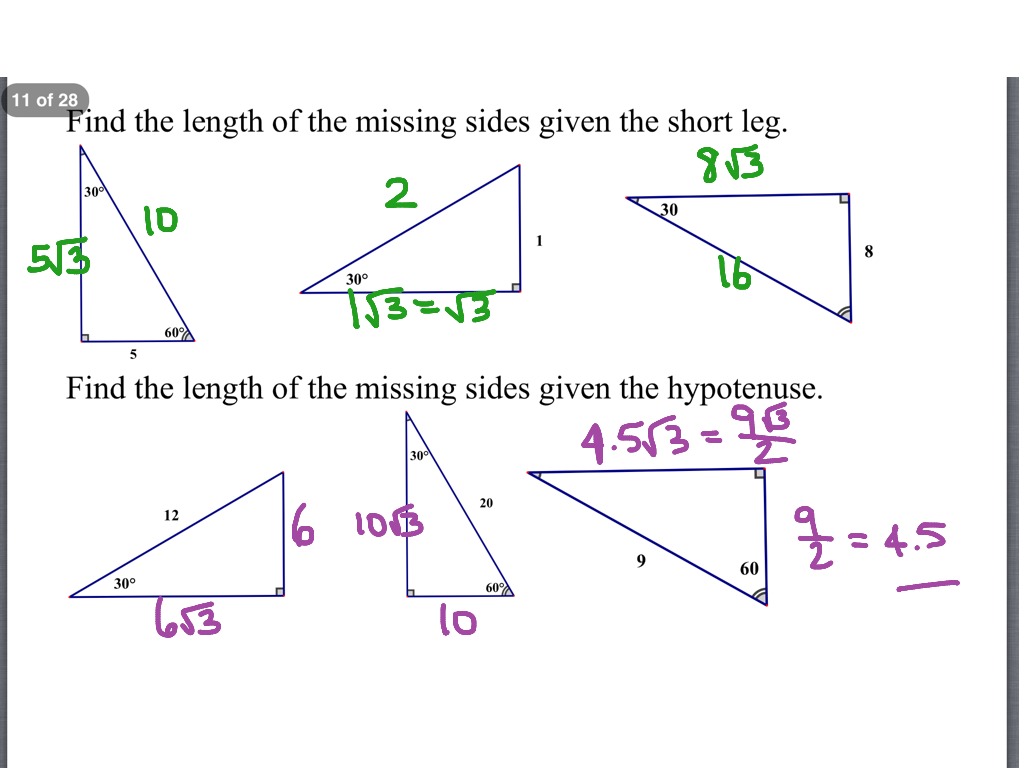
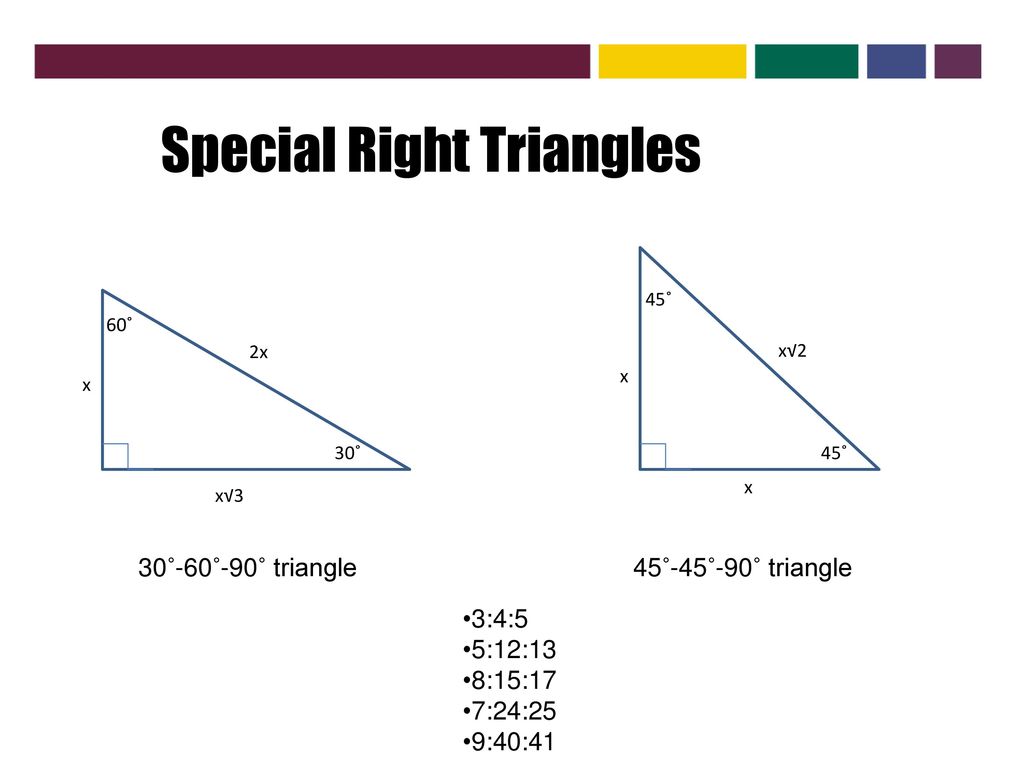
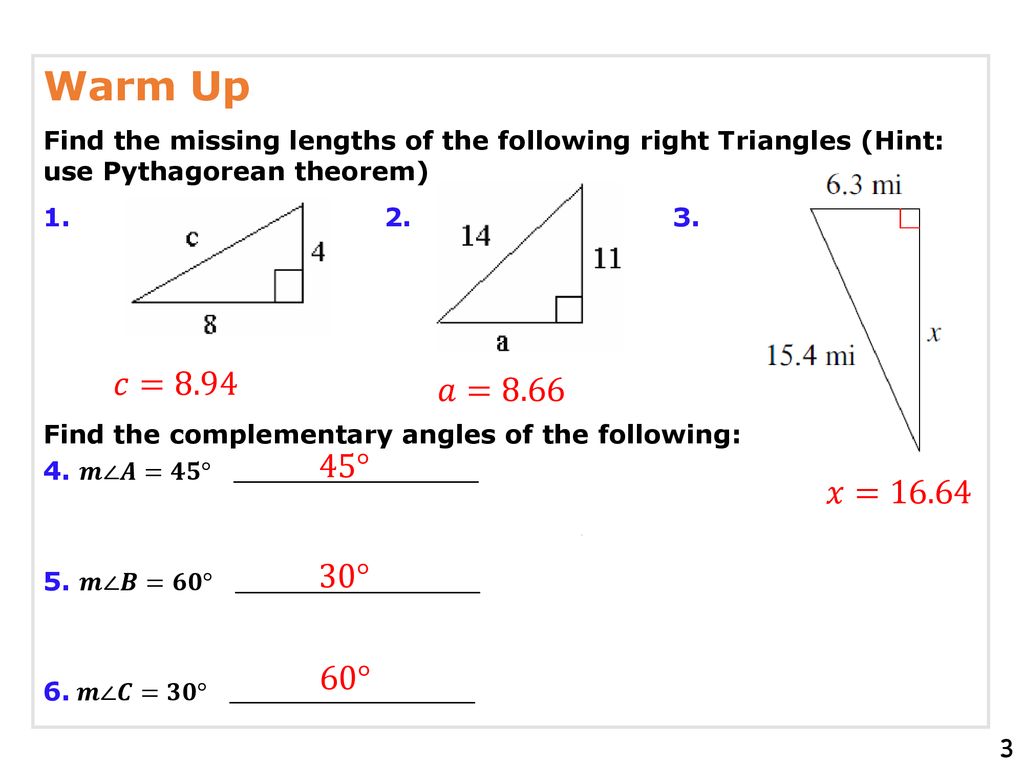
The 5 12 13 triangle is an SSS special right triangle with the ratio between its side lengths as 5, 12, and 13 It is a common Pythagorean triple that is worth memorizing to save time when dealing with right triangles The other common SSS special right triangle is the 3 4 5 triangle18 The diagonal of a rectangle is 12 in and intersect at an angle to make a 60° angle Find the perimeter of the rectangle Geometric Mean 19 Find x 21 Find x 22 Find x 23 24 45˚ 8 45˚ 15 60˚ 24 45˚ 7 J L Q 30° x 9 R 60˚ 30˚ 28 18 30˚ 40 50 7 9 x 30 6 x 9 x 3This tool is designed to find the sides, angles, area and perimeter of any right triangle if you input any 3 fields (any 3 combination between sides and angles) of the 5 sides and angles available in the form

How To Use The 3 4 5 Rule To Build Square Corners 4 Steps
3 4 5 special right triangle angles
3 4 5 special right triangle angles-Understand the 345 method If a triangle has sides measuring 3, 4, and 5 feet (or any other unit), it must be a right triangle with a 90º angle between the short sides If you can "find" this triangle in your corner, you know the corner is square This is based on the Pythagorean Theorem from geometry A 2 B 2 = C 2 for a right triangle CI 345 II III IV but there are many others V If 3 of the 4 elements are provided then the 4th can be derived Even if 3 side lengths 3, 4, and 5 are given then it must be a right triangle VI All side lengths can be scaled They just must remain in the same ratio 2 The and degree right triangles



Trigonometric Functions Precalculus Chapter 4 4 1 Special Right Triangles And Trigonometric Ratios Math 1330 Precalculus 345 Chapter 4 5 2 T Find The Six Trigonometric Functions
A right triangle has one angle equal to 90 degrees A right triangle can also be an isosceles trianglewhich means that it has two sides that are equal A right isosceles triangle has a 90degree angle and two 45degree angles One of the most famous is the "3, 4, 5 triangle" The Egyptians used this triangle for land surveying SomeIn a degrees right triangle, the side opposite the 30degree angle is Use the and triangle relationships to solve for the missing sides Use the answers to reveal the name of the team that Abraham M Saperstein established and sent on the road in 1927That is, the sum of the two acute angles in a right triangle is equal to #90^o# If we know one of these angles, we can easily substitute that value and find the missing one For example, if one of the angles in a right triangle is #25^o#, the other acute angle is given by #25^o y=90^o# #y=90^o25^o# #y=65^o#
345 and triangles are special right triangles defined by their side lengths The numbers 345 and describe the lengths of the triangle's legs, meaning that, when you have a right triangle with one leg length 4 and with a hypotenuse length 5, then you automatically know that the third leg equals 3A) 328 b) 575 c) 377 d) 303 Question 4 In the right triangle ABC below, angle A measures 30° and the length of AC is 8 unitsNo, a right triangle cannot have all 3 sides equal, as all three angles cannot also be equal, as one has to be 90° by definition A right triangle can, however, have its two nonhypotenuse sides be equal in length This would also mean the two other angles are equal to 45°
A right triangle is any triangle with one right angle of 90 o There are several kinds of right triangles, but the 345 right triangle has special characteristics The measurements of the sidesIn a right triangle, the measure of one of the angles is 49° and the hypotenuse has a length of 50 cm Which of the following is the nearest approximation to the length, in cm, of the leg opposite to this angle?Math Warehouse's popular online triangle calculator Enter any valid combination of sides/angles(3 sides, 2 sides and an angle or 2 angle and a 1 side) , and our calculator will do the rest!



Identifying Types Of Polygons Activity
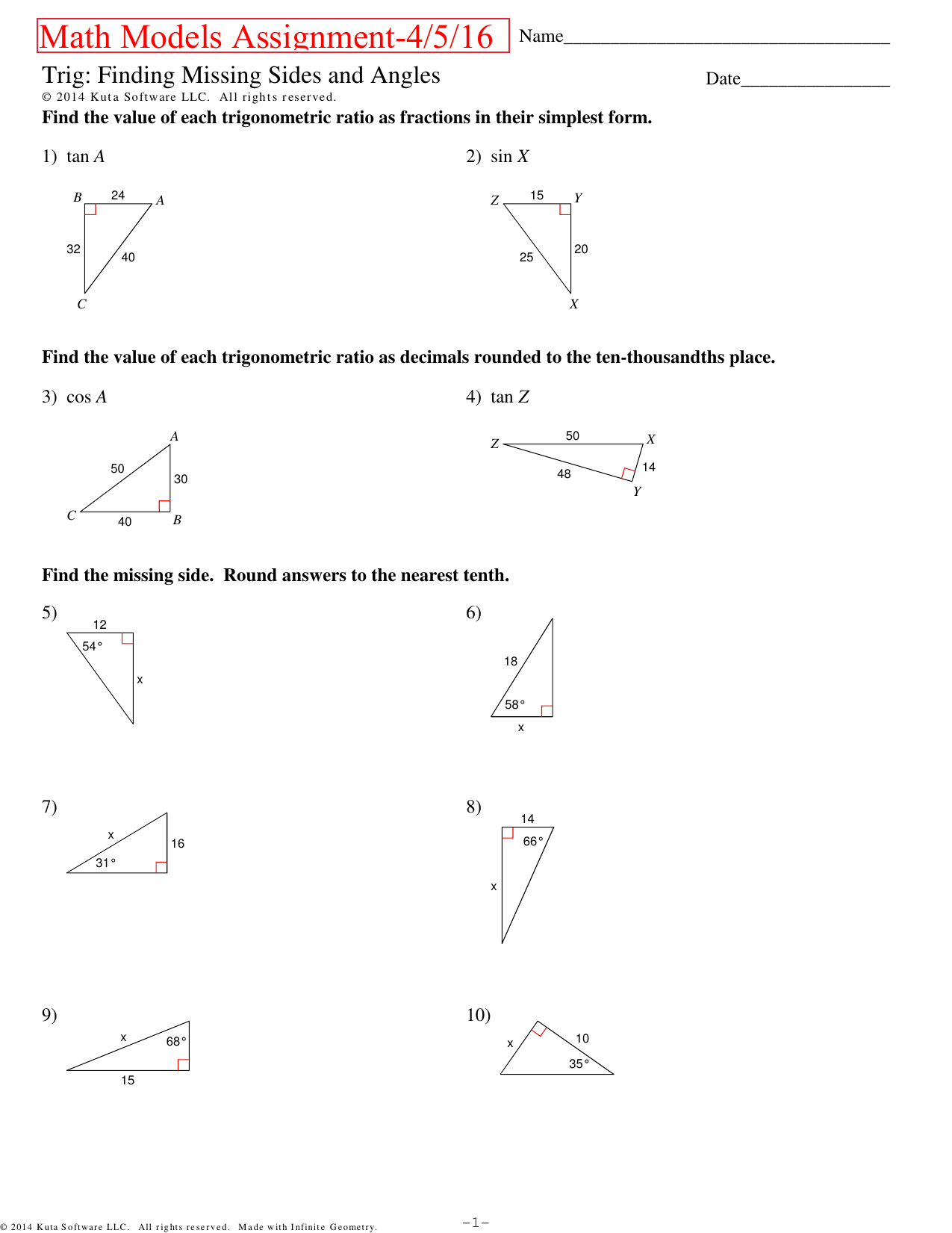


7 Solvingrighttriangles
The 3 4 5 triangles are the only right triangles with edges in arithmetic progressionTriangles based on Pythagorean triples are Heronian, meaning they have integer area as well as integer sides The possible use of the 3 4 5 triangle in Ancient Egypt, with the supposed use of a knotted rope to lay out such a triangle, and the question whether Pythagoras' theorem was known at thatHow does this right triangle calculator work?Understand the 345 method If a triangle has sides measuring 3, 4, and 5 feet (or any other unit), it must be a right triangle with a 90º angle between the short sides If you can "find" this triangle in your corner, you know the corner is square This is based on the Pythagorean Theorem from geometry A 2 B 2 = C 2 for a right triangle C


Arxiv Org Pdf 1706



New Sat Trigonometry 10 Practice Questions 19 Youtube
We have to use the sine rule here If the triangle is ABC we have angles A, B and C and sides AB, BC and CA The rule says that AB/sin(C) = BC/sin(A) = CA/sin(B) In a 345 triangle = ABBCCA we know CA = 5 is the hypotenuse and its opposite angWhen the angle of elevation is 45°, we get a 45°45°90° special right triangle By 45°45°90° Triangle Theorem, we have Hypotenuse = √2 ⋅ Leg 70 = √2 ⋅ h Divide each side by √2 70 / √2 = h Use calculator to approximate 495 ≈ h When the angle of elevation is 30°, the ramp height is 35 feet345 Right Triangle A 345 triangle is right triangle whose lengths are in the ratio of 345 When you are given the lengths of two sides of a right triangle, check the ratio of the lengths to see if it fits the 345 ratio Side1 Side2 Hypotenuse = 3n 4n 5n Solve problems with 345 right triangles Example 1


Www Polk K12 Ga Us Userfiles 55 Classes t 12 ch9 trig functions v2 Pdf


Scholarworks Umt Edu Cgi Viewcontent Cgi Article 1240 Context Utpp
1) Using the special 345 right triangle, you can infer that the missing hypotenuse is 5 2) By using the Pythagorean Theorem, you can solve for the length of the hypotenuse In this case 2 Using the meaning of congruent (the exact same three angles and sides), determine if these two triangles fit this meaningThis extensive collection of worksheets on triangles for grades 3 through highschool is incredibly useful in imparting a clear understanding of a variety of topics like classifying triangles, similar triangles, congruence of triangles, median and centroid of a triangle, inequality theorem, Pythagorean inequalities, area, perimeter and angles in a triangle and much moreIn this situation right over here, actually a 3, 4, 5 triangle, a triangle that has lengths of 3, 4, and 5 actually is a right triangle And this right over here would be a 90 degree angle You could have an equilateral acute triangle



3 Ways To Find The Length Of The Hypotenuse Wikihow


Q Tbn And9gcrfviva8aik6sfaebzrvu1sb760sjxfcy8idaurb9fj73mcr Uo Usqp Cau
There are also special right triangles triangle (isosceles right triangle) a triangle with one right angle and two 45degree angles Both legs are equal in length, and the ratio of its sides is xx√2x right triangle interior angles are 30, 60, and 90 degreesA 3 4 5 triangle is an SSS right triangle (meaning we know the three side lengths) If we know two of the side lengths and they are congruent with the 3 4 5 ratio, we can easily determine the third side length by using the ratio The other common SSS special right triangle is the 5 12 13 triangleSpecial right triangles proof (part 2) Practice Special right triangles triangle example problem Area of a regular hexagon Special right triangles review This is the currently selected item Next lesson Ratios in right triangles Sort by Top Voted Area of a regular hexagon



How To Use The 3 4 5 Rule To Build Square Corners 4 Steps
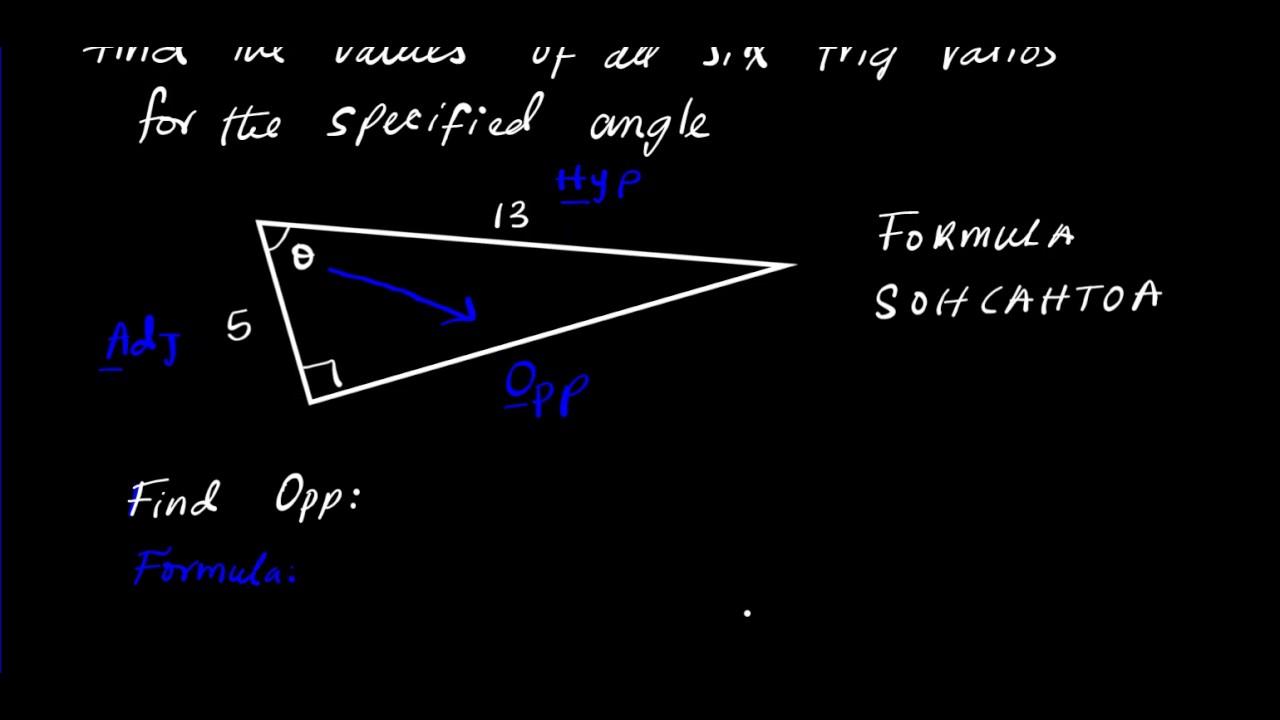


Finding Values Of All Six Trig Functions Right Triangle Youtube
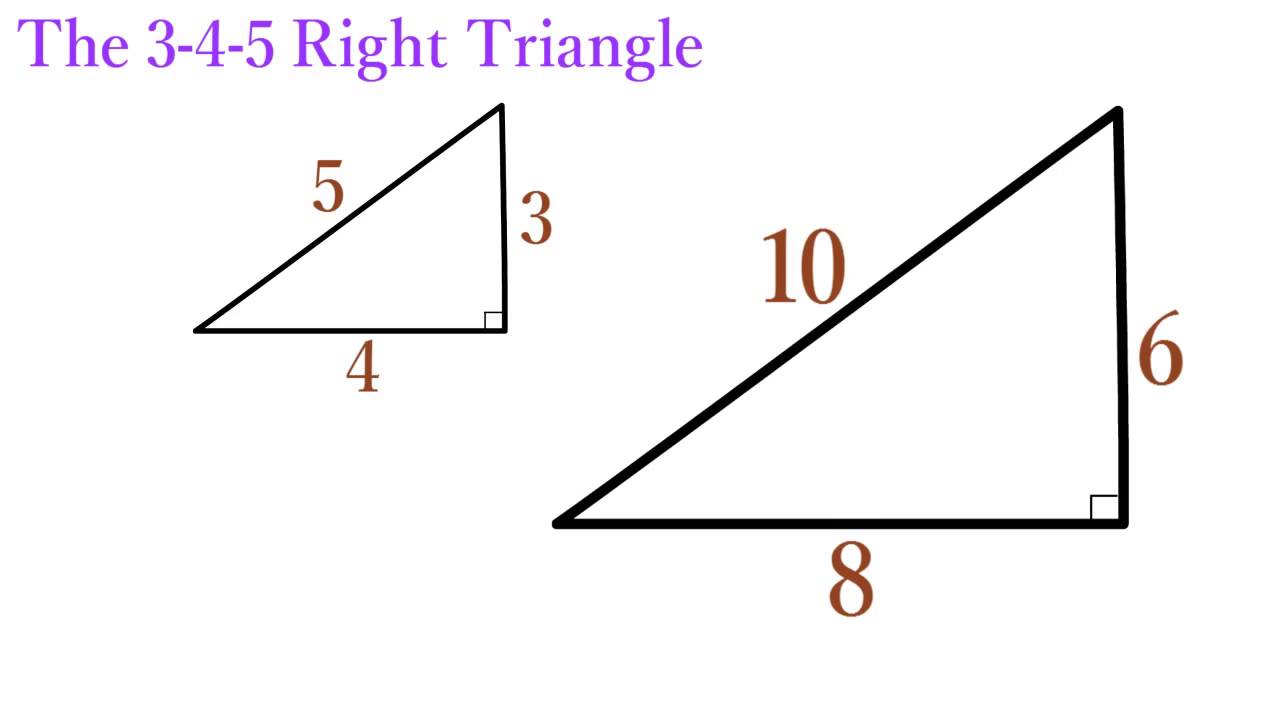
If you multiply the sides by any number, the result will still be a right triangle whose sides are in the ratio 345 For example 6, 8, and 10 Interior Angles Because it is a right triangle one angle is obviously 90° The other two are approximately 3687° and 5313°Section 33 Right Triangles The origins of right triangle geometry can be traced back to 3000 BC in Ancient Egypt The Egyptians used special right triangles to survey land by measuring out 345 right triangles to make right angles The Egyptians mostly understood right triangles in terms of ratios or what3 3 Letter Key 01 2 3 H 4 5 L 6 N 7 R 8 s 9 162 5) X—24—25 is a special one 6) 3—X—5 is a special one SOLUTIONS Right angles are 90 degrees In a fight triangle, the length of the hypotenuse is twice the measure of the small side opposite th 30 egree angle Use Pythagorean Theorem = (N50)2 Since 2 sides are congruent, this



Special Right Triangles Worksheets Triangle Worksheet Trigonometry Worksheets Word Problem Worksheets


Www Rcsdk12 Org Cms Lib04 Ny Centricity Domain 61 7 2 special right triangles and pt Pdf
Isosceles triangles have 2 equal sides and 2 equal angles 3 Rightangled 1 of the angles is a right angle (90°) in rightangled triangles 4 Scalene Scalene triangles have no equal sides andG25 Explain and use angle and side relationships in problems with special right triangles, such as 30°, 60°, and 90° triangles and 45°, 45°, and 90° trianglesI 345 II III IV but there are many others V If 3 of the 4 elements are provided then the 4th can be derived Even if 3 side lengths 3, 4, and 5 are given then it must be a right triangle VI All side lengths can be scaled They just must remain in the same ratio 2 The and degree right triangles


Www Cabarrus K12 Nc Us Cms Lib Nc Centricity Domain 7914 Unit 5 right triangles notes key Pdf



3 4 5 Right Triangles Explanation Examples
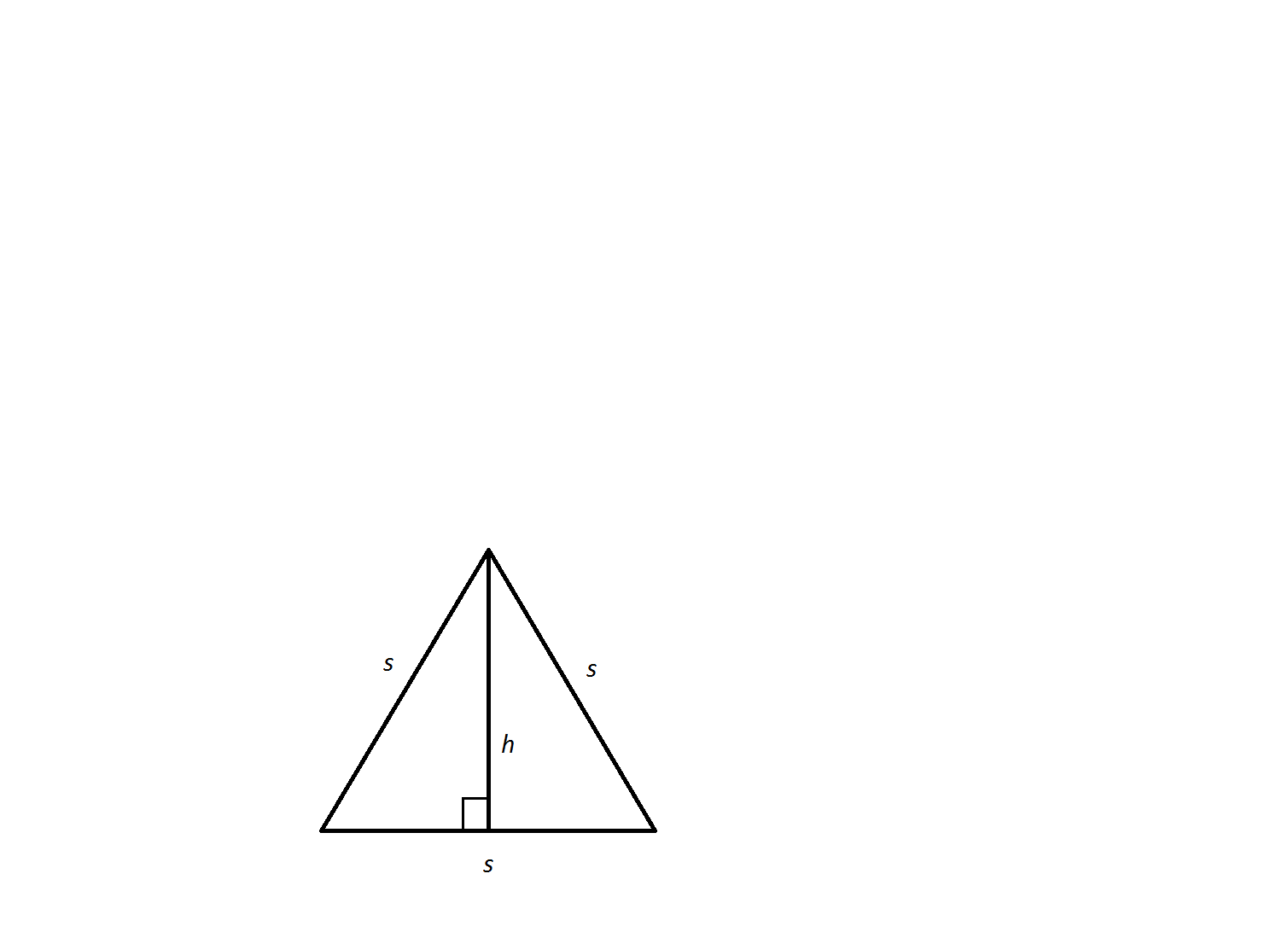
The two sides have measures of 3 and 3 Example 2 If the diagonal of a square is 6 , find the length of each of its sides Method 1 The diagonal of a square divides it into two congruent isosceles right trianglesLook at Figure 3 Figure 3 A diagonal of a square helps create two congruent isosceles right triangles The ratio x x x for isosceles right triangles can now be appliedThis math lesson looks at pythagorean math how to work out the unknown sides of right angles triangle The 3,4,5 triangle will also be explored Become a mDraw an arc 400 away from the start of the 300 line Draw an arc 500 away from the end of the 300 line Connect from the start of the 300 line to where the arcs cross And you have your "3,4,5" triangle with its right angle


Http Mathwithmills Weebly Com Uploads 8 6 0 2 Geometry Unit 7 Note Sheets Pdf



Trig Ratios Right Triangle Trigonometry Vividmath Com Youtube
1) Using the special 345 right triangle, you can infer that the missing hypotenuse is 5 2) By using the Pythagorean Theorem, you can solve for the length of the hypotenuse In this case 2 Using the meaning of congruent (the exact same three angles and sides), determine if these two triangles fit this meaningSo we could say that the sum of the angles of a triangle add up to, instead of saying 180 degrees, 180 degrees is the same thing as pi radians So this angle plus that angle are going to add up to pi So lets just say that this right over here, lets just say measure of angle ABD in radians, plus pi over four, plus, this is a right angleIt will even tell you if more than 1 triangle can be created


Www Cabarrus K12 Nc Us Cms Lib Nc Centricity Domain 7914 Unit 5 right triangles notes key Pdf



3 Ways To Find The Height Of A Triangle Wikihow


Www Cabarrus K12 Nc Us Cms Lib Nc Centricity Domain 7914 Unit 5 right triangles notes key Pdf



Proportional Relationships In Triangles Video Lesson Transcript Study Com



How To Find The Area Of A Right Triangle Basic Geometry
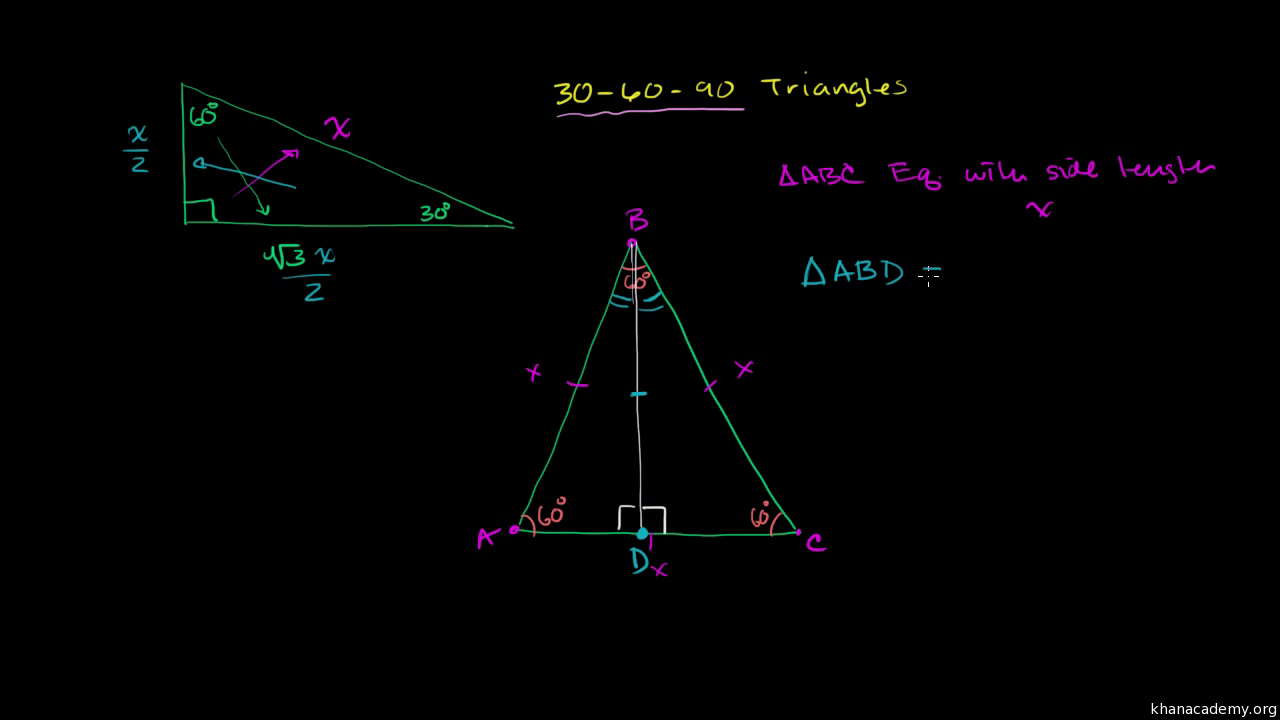


Special Right Triangles Proof Part 1 Video Khan Academy



How Many Triangles Do You See Viral Math Problem Triangle


Q Tbn And9gcrrf9tt 2mqa Bszgqwpe1q Xurir1q9paiktyme8vvbqmjguxj Usqp Cau



How To Find The Length Of The Hypotenuse Of A Right Triangle Pythagorean Theorem Basic Geometry



Triangle Wikipedia


Www Cabarrus K12 Nc Us Cms Lib Nc Centricity Domain 7914 Unit 5 right triangles notes key Pdf



Special Right Triangles Proof Part 1 Video Khan Academy
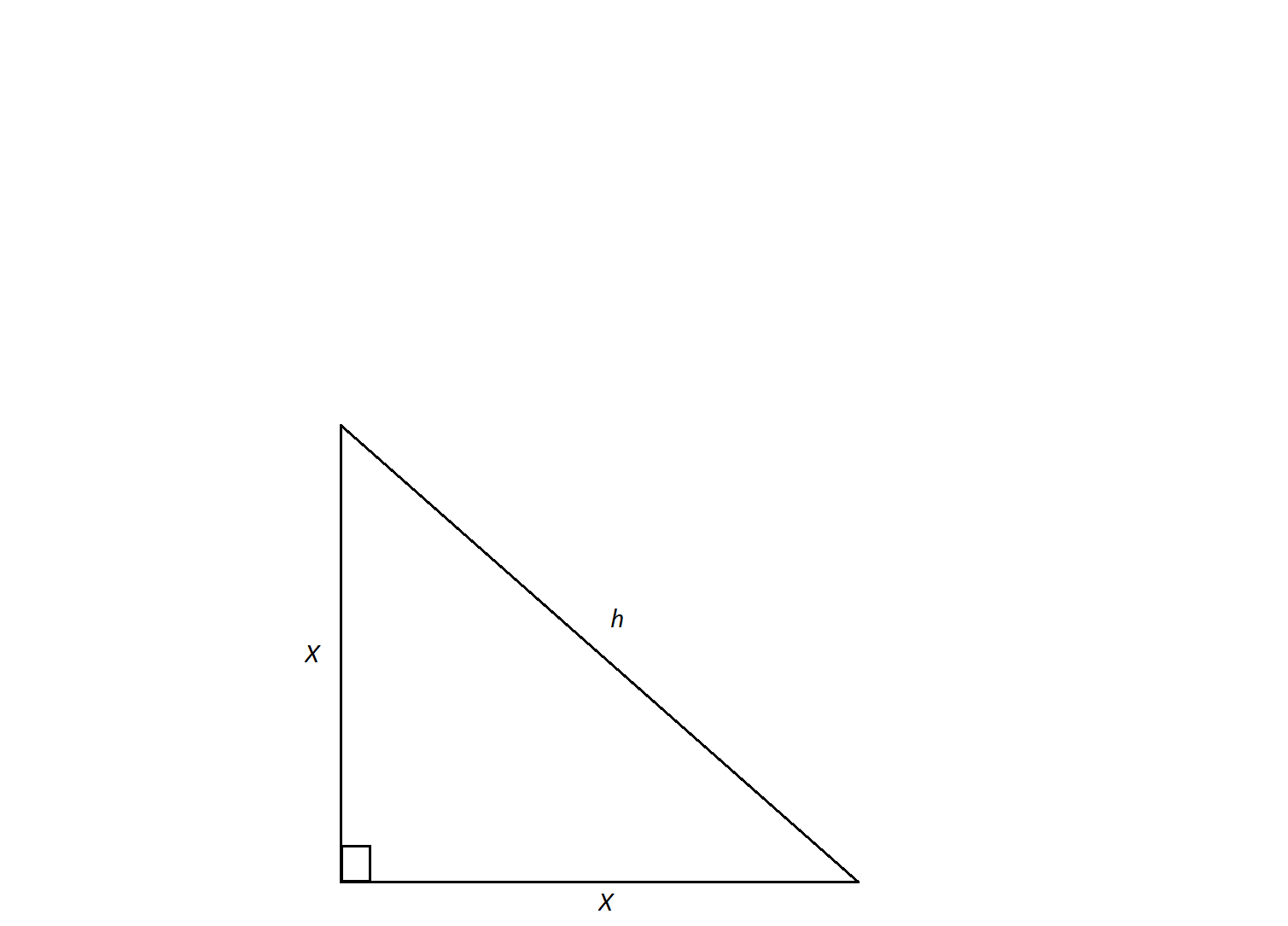


How To Find The Perimeter Of A 45 45 90 Right Isosceles Triangle High School Math


Www Portnet Org Cms Lib6 Ny Centricity Domain 276 Right triangle trigonometry Pdf



Gebhard Curt Geometry Unit 8 Right Trig



Special Right Triangles Solutions Examples Videos



Trigonometric Functions Manualzz



Chapter 7 Right Triangles Trigonometry



List Of Trigonometric Identities Wikipedia


Www Montgomerycollege Edu Documents Academics Support Learning Centers Ackerman Learning Center Rockville Recreate The Unit Circle Pdf


Http Www Radford Edu Wacase Math 116 supplemental text pythagorean thm



Triangles


Q Tbn And9gctfu3psrecfuubzqh 9zbmxn5ivaeypypfgfb14jy7b4isorjln Usqp Cau



Right Triangles Math Mistakes


Www Nuffieldfoundation Org Sites Default Files Files Fsma geometrical design student Pdf


7 3 Videob Math Geometry Special Right Triangles Showme
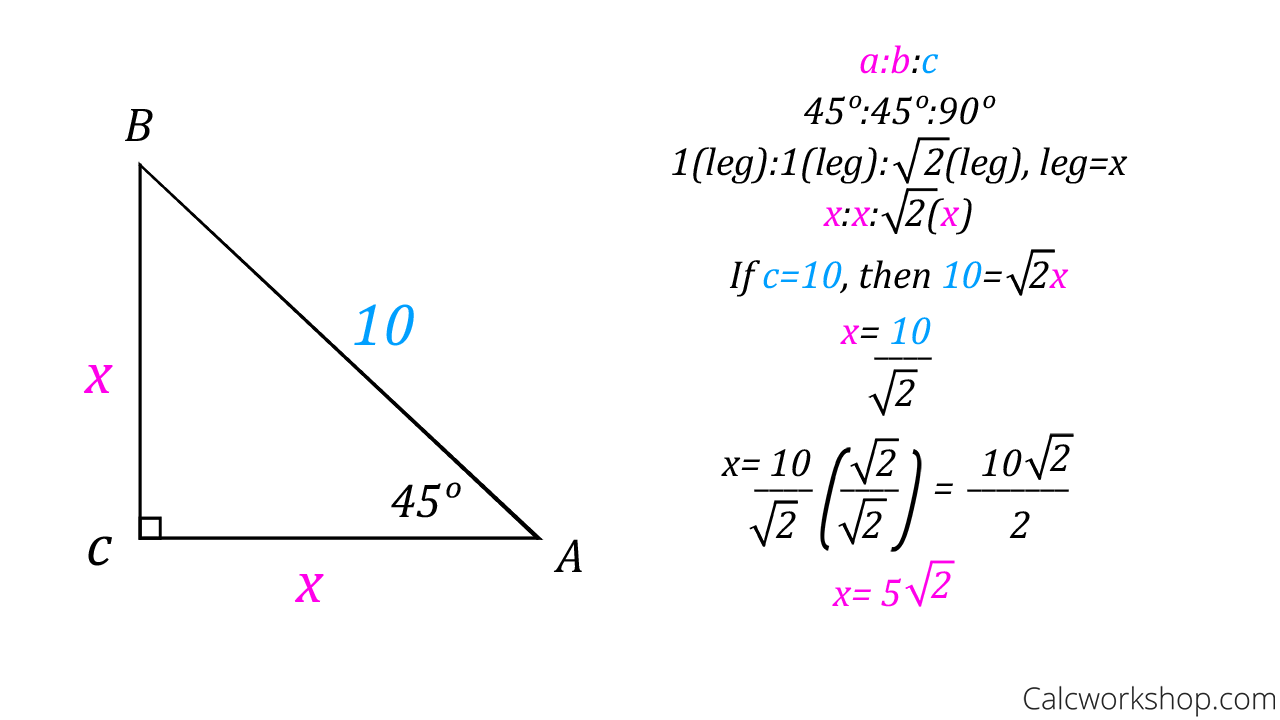


Special Right Triangles Fully Explained W 19 Examples



For Each Question Use The Diagram And The Information Given To Find All The Unknown Angles


How To Find The Area Of An Equilateral Triangle High School Math



Trigonometric Functions Precalculus Chapter 4 4 1 Special Right Triangles And Trigonometric Ratios Math 1330 Precalculus 345 Chapter 4 5 2 T Find The Six Trigonometric Functions



3 Ways To Find The Length Of The Hypotenuse Wikihow



1 Math 116 Supplemental Textbook Pythagorean Theorem Pdf Free Download



Geometry Welcome To Mrs Bietler S Website



45 45 90 Right Triangles Solutions Examples Videos
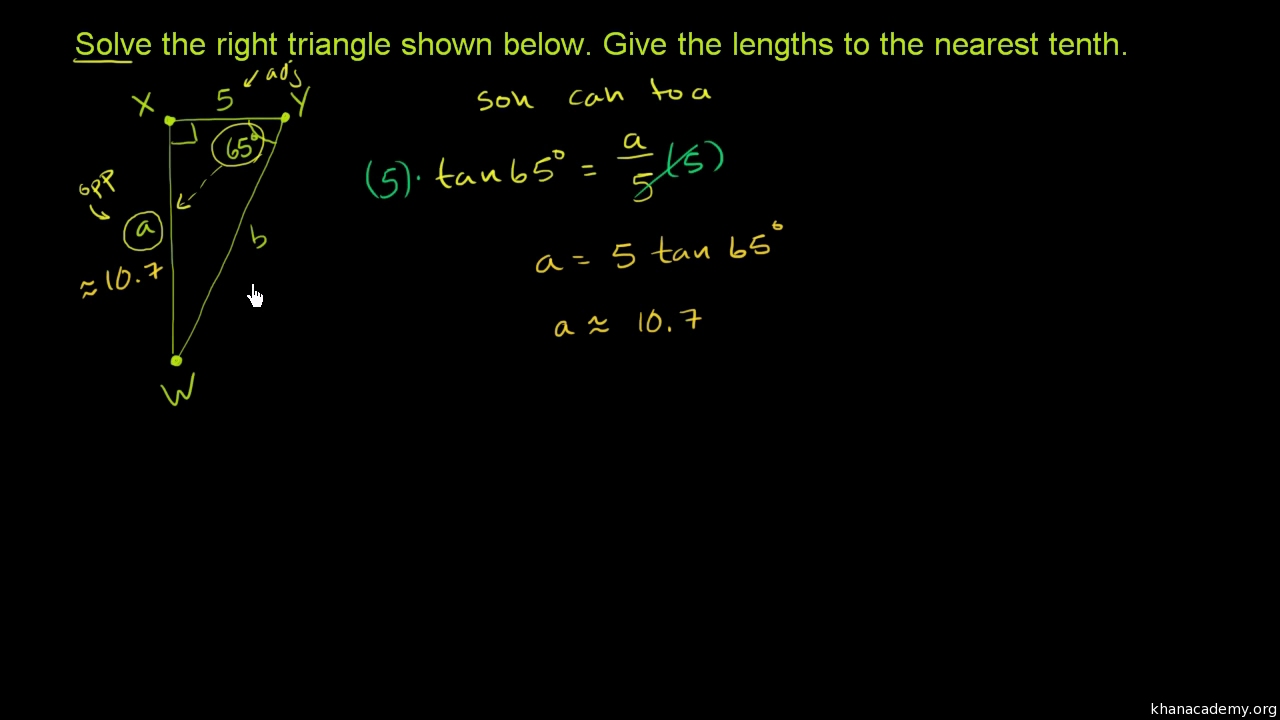


Solving For A Side In Right Triangles With Trigonometry Video Khan Academy


Plane Geometry Properties And Relations Of Plane Figures Ppt Download



Right Triangles Math Mistakes



Special Right Triangles Mazes Special Right Triangle Right Triangle Teaching Geometry
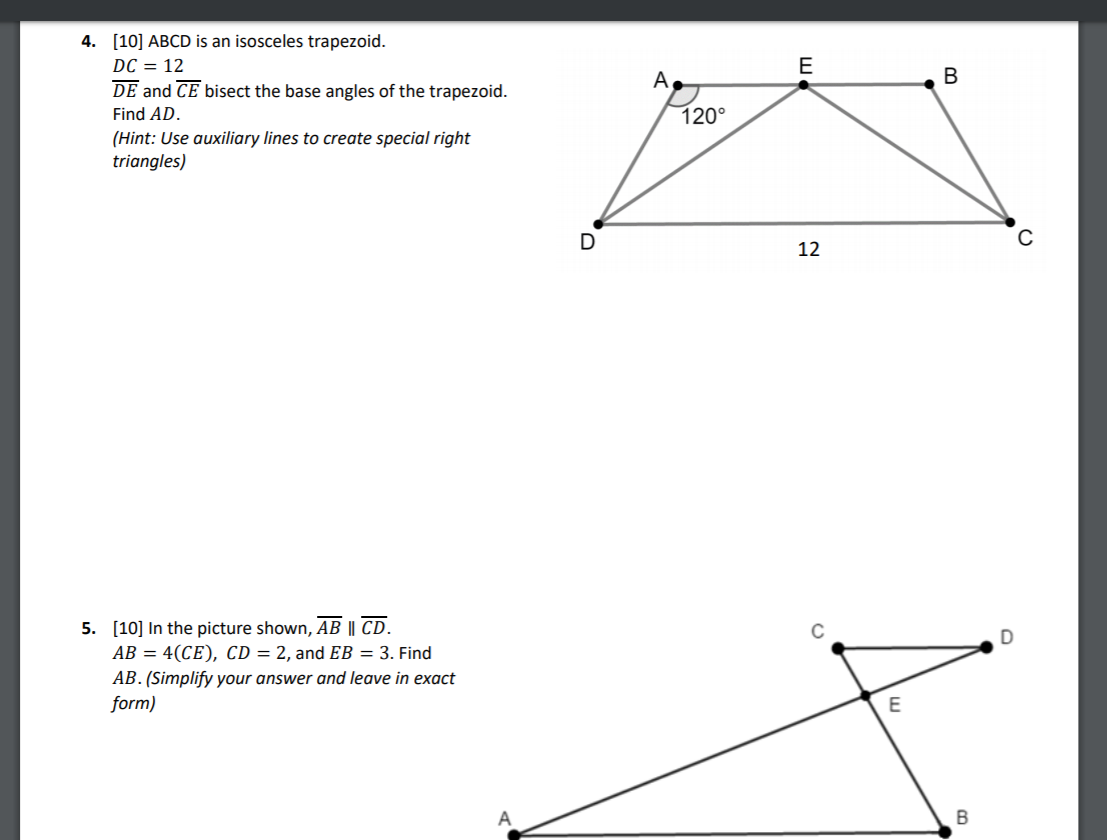


Solved E A B 4 10 Abcd Is An Isosceles Trapezoid Dc Chegg Com
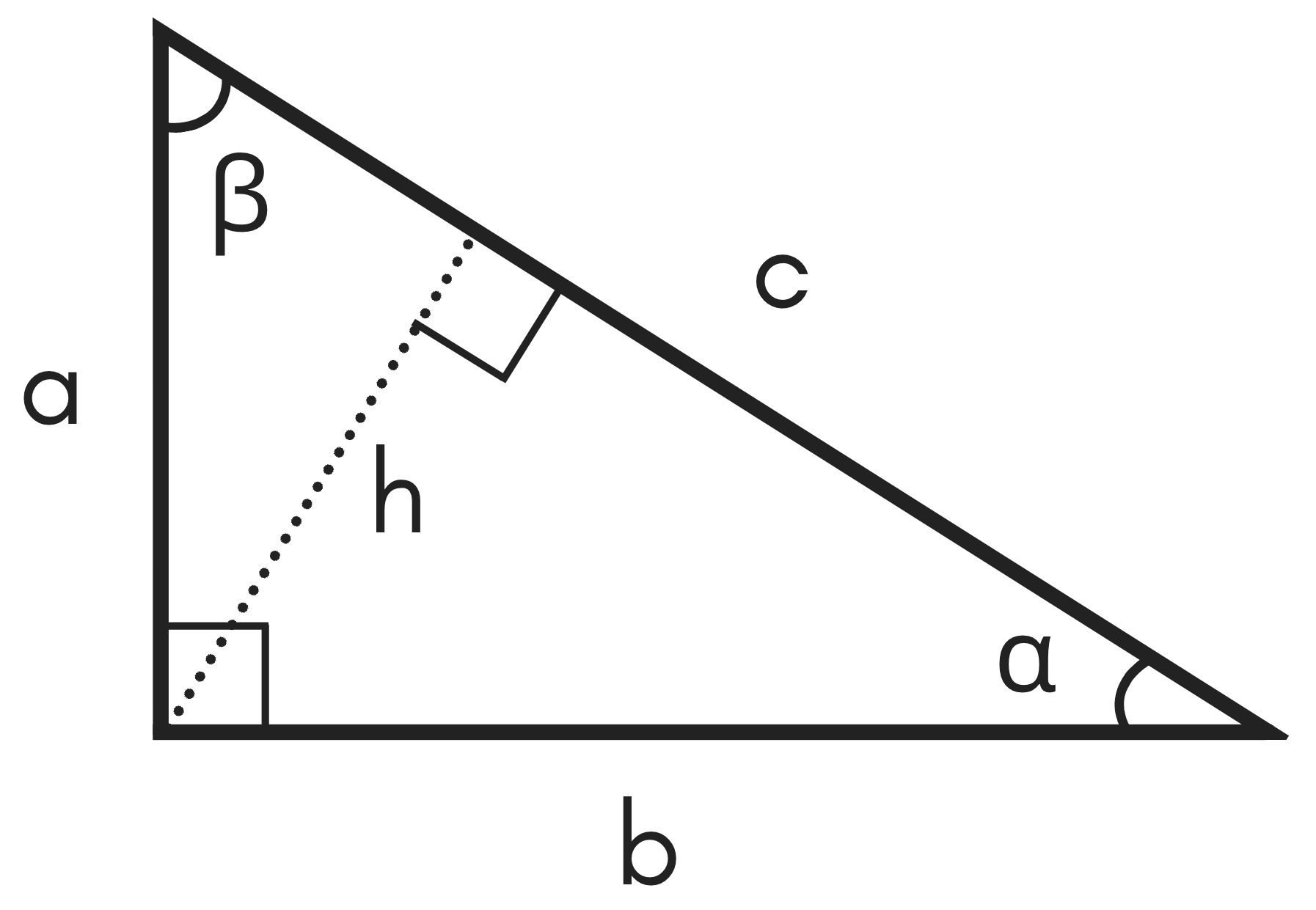


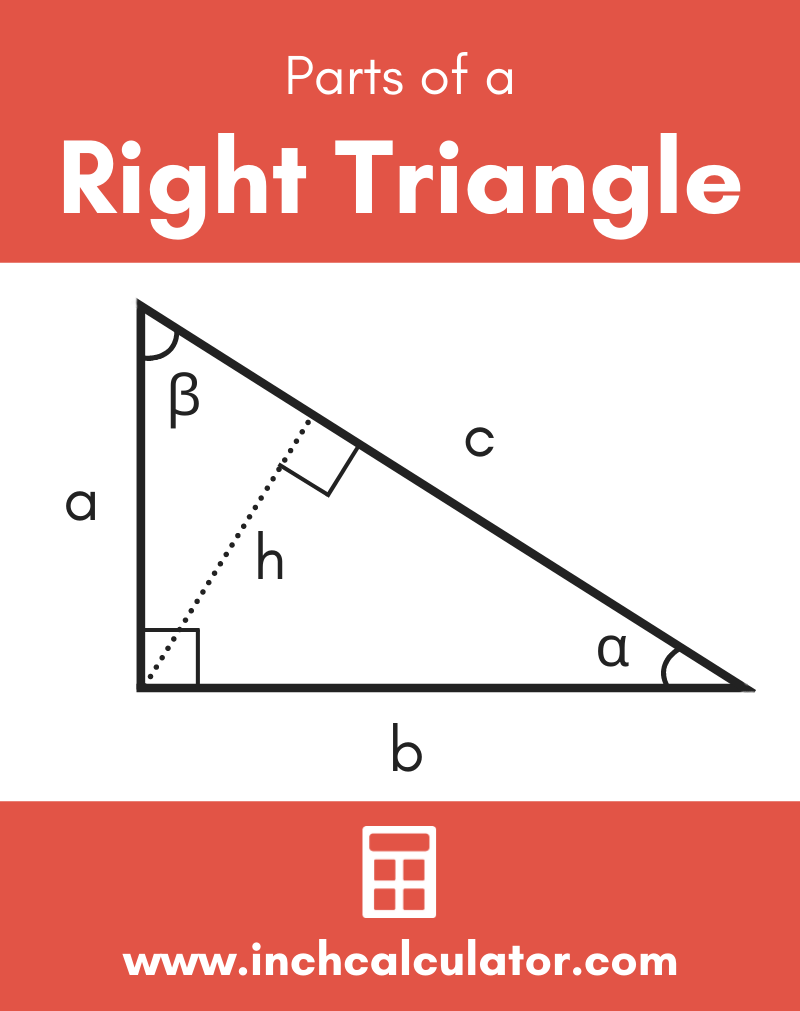
Right Triangle Calculator Solve Any Edge Or Angle Inch Calculator
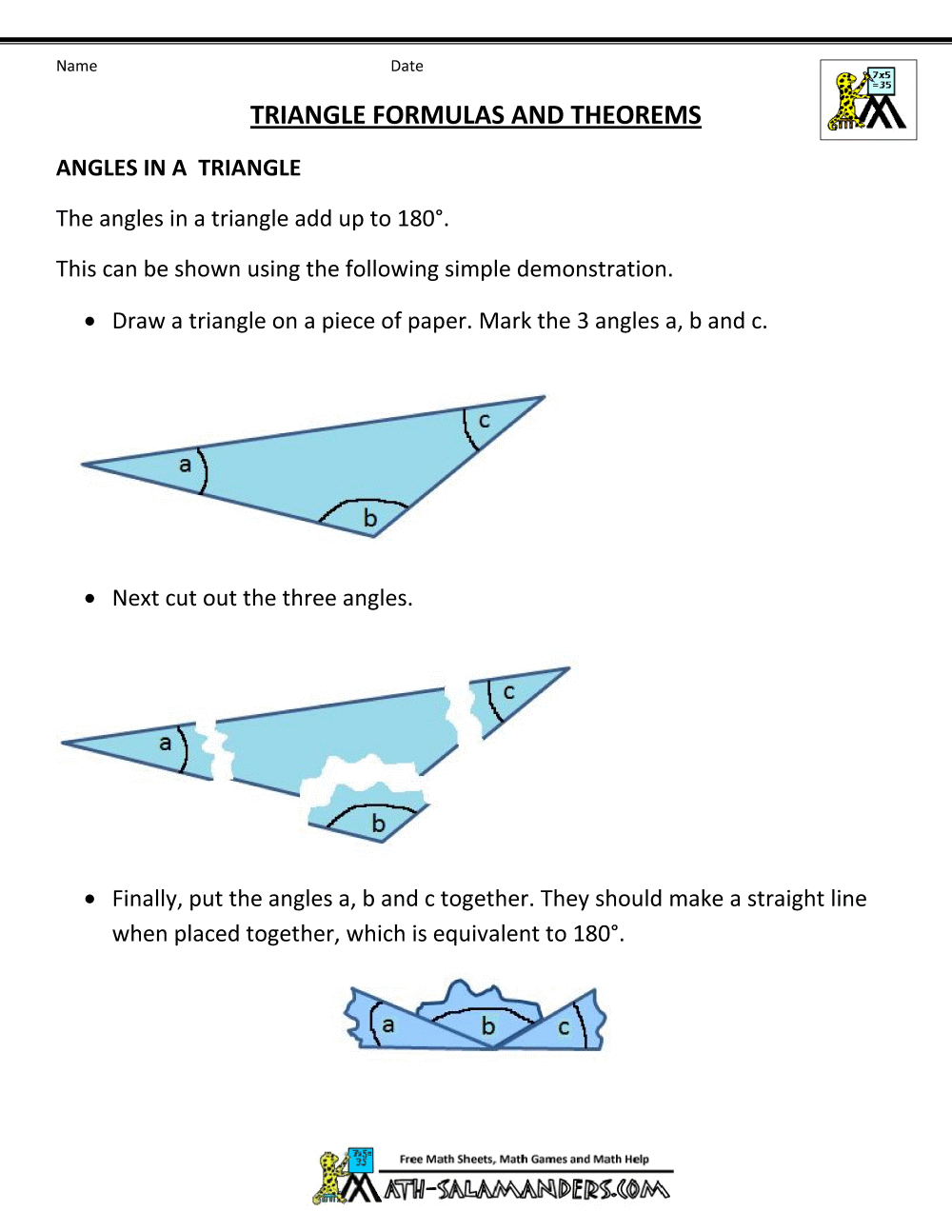


Geometry Formulas Triangles



Trigonometry Is Essential To Physics Here Are The Basics Wired


Geometry Summary Angles



Intro To The Trigonometric Ratios Video Khan Academy



Integer Triangle Wikipedia



Special Right Triangles Fully Explained W 19 Examples



Right Triangles Math Mistakes



30 60 90 Triangle Theorem Ratio Formula Video



Right Triangle Wikipedia


Module 13 Trigonometry With Right Triangles Ppt Download


Www Cabarrus K12 Nc Us Cms Lib Nc Centricity Domain 7914 Unit 5 right triangles notes key Pdf


Http Mrmuscarella Weebly Com Uploads 2 2 8 3 Ch 7 Notepacket Right Triangles And Trig Pdf


Lesson 12 The 3 4 5 Right Triangle Simplestep Learning Youtube


How To Find The Length Of The Hypotenuse Of A Right Triangle Pythagorean Theorem Basic Geometry


Www Cabarrus K12 Nc Us Cms Lib Nc Centricity Domain 7914 Unit 5 right triangles notes key Pdf


Right Triangle Calculator Solve Any Edge Or Angle Inch Calculator


Http Www2 Mae Ufl Edu Uhk Triplets Pdf
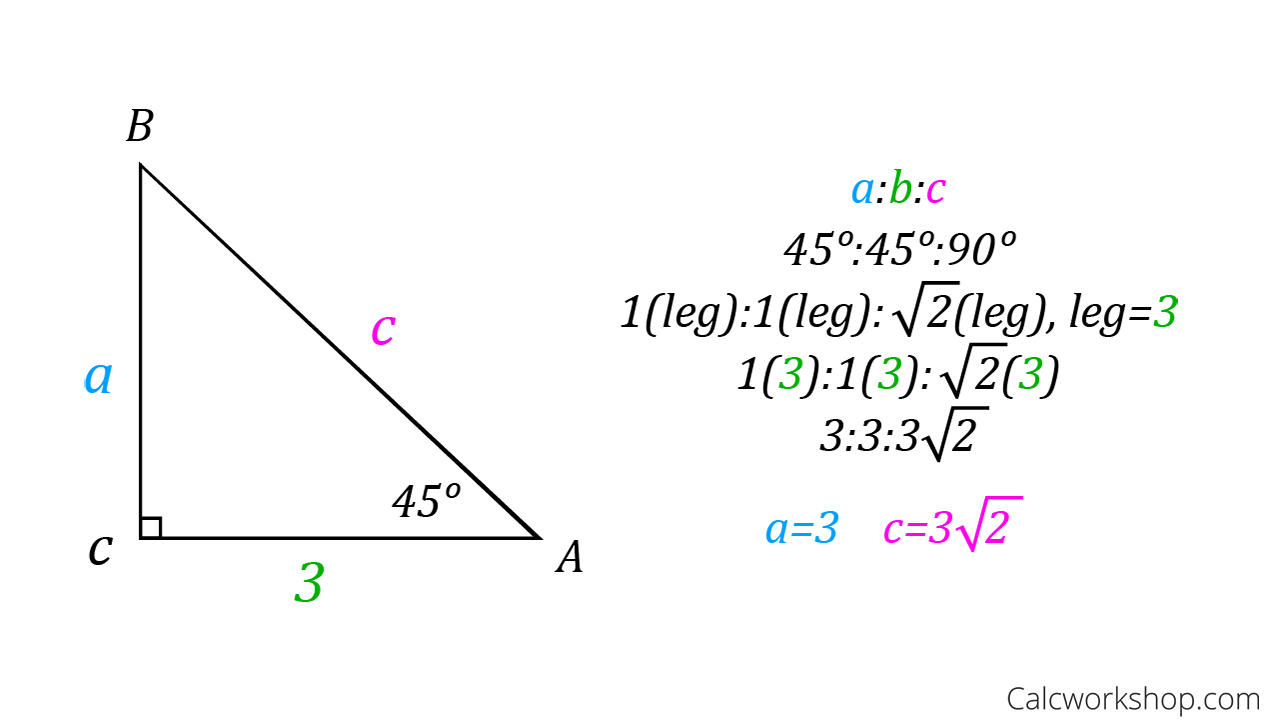


Special Right Triangles Fully Explained W 19 Examples
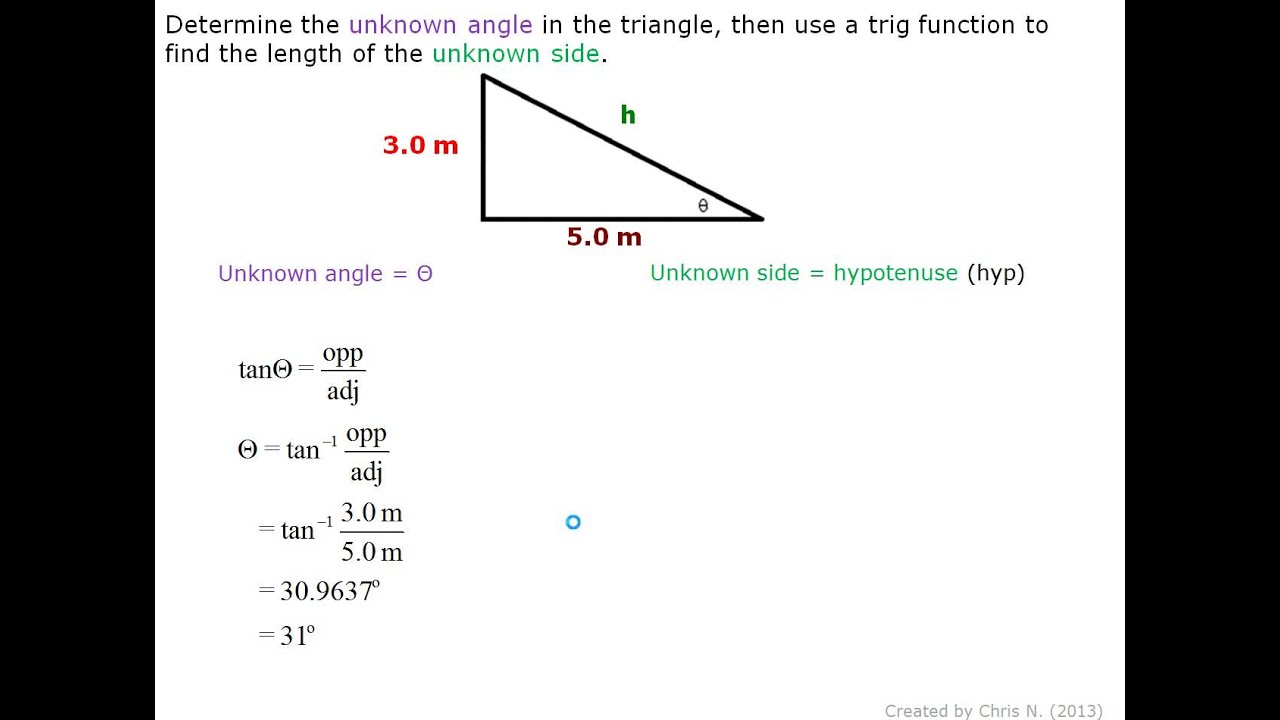


Using Sides To Find Angles In A Right Triangle Youtube


What Is A Triangle And Its Properties Definition Types Formulas Of Triangles
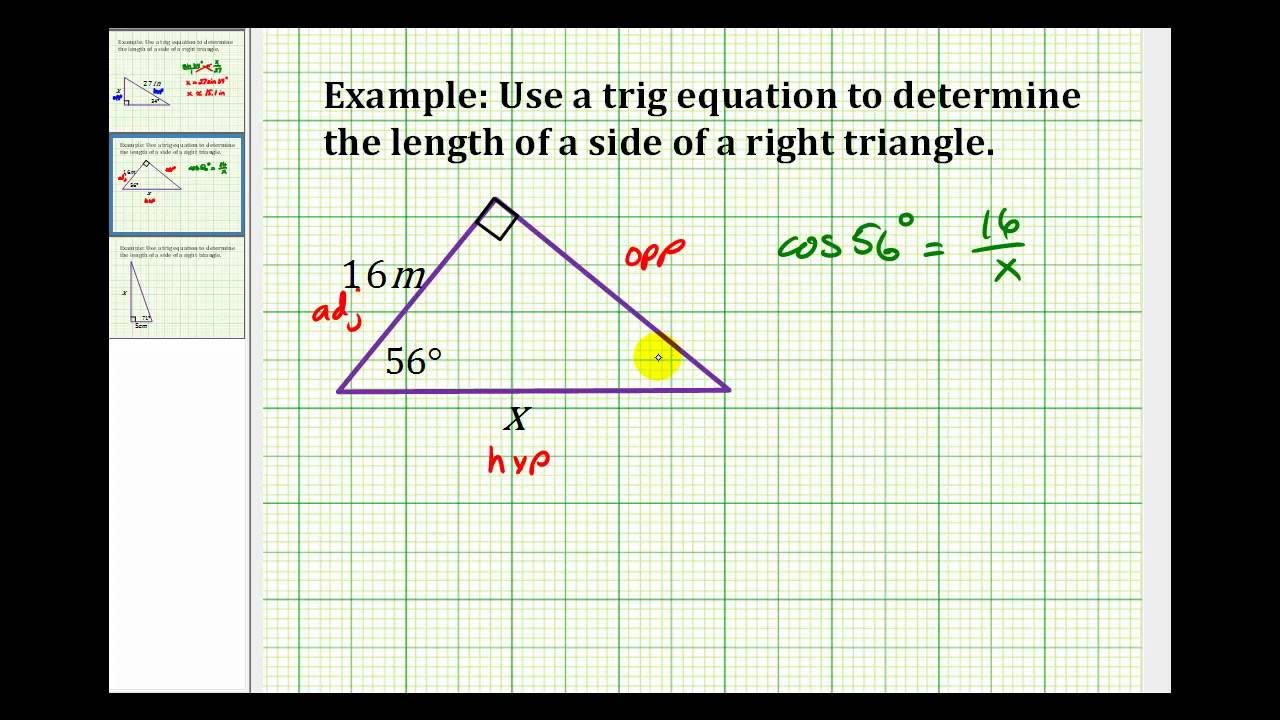


Right Triangle Trigonometry Precalculus Ii


Q Tbn And9gcq2z310vkycaowv90uyh8eiso2xd1jbhd0mr16tlcdd7r6zdvqf Usqp Cau



Unit 7 Day 4 Video Notes
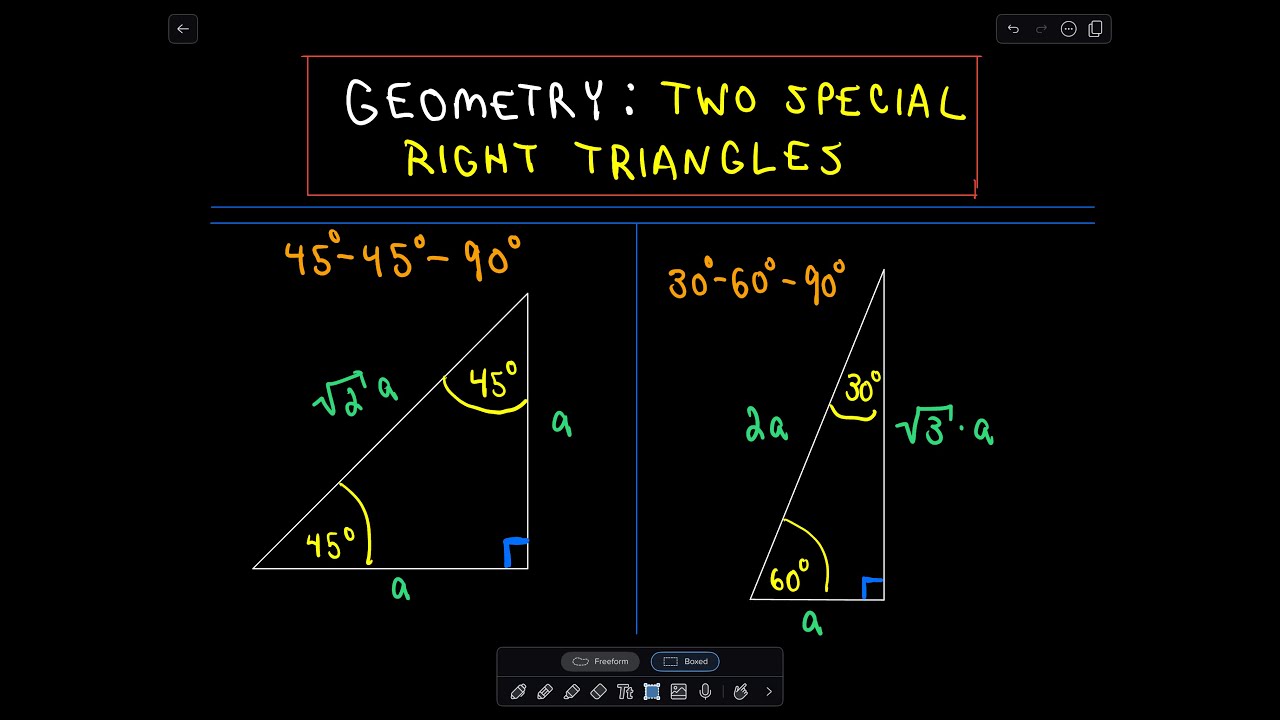


Special Right Triangles Solutions Examples Videos



Kutasoftware Geometry Special Right Triangles Part 1 Youtube



Right Triangles Math Mistakes



Right Triangle Trigonometry Precalculus Ii



Right Triangles Math Mistakes
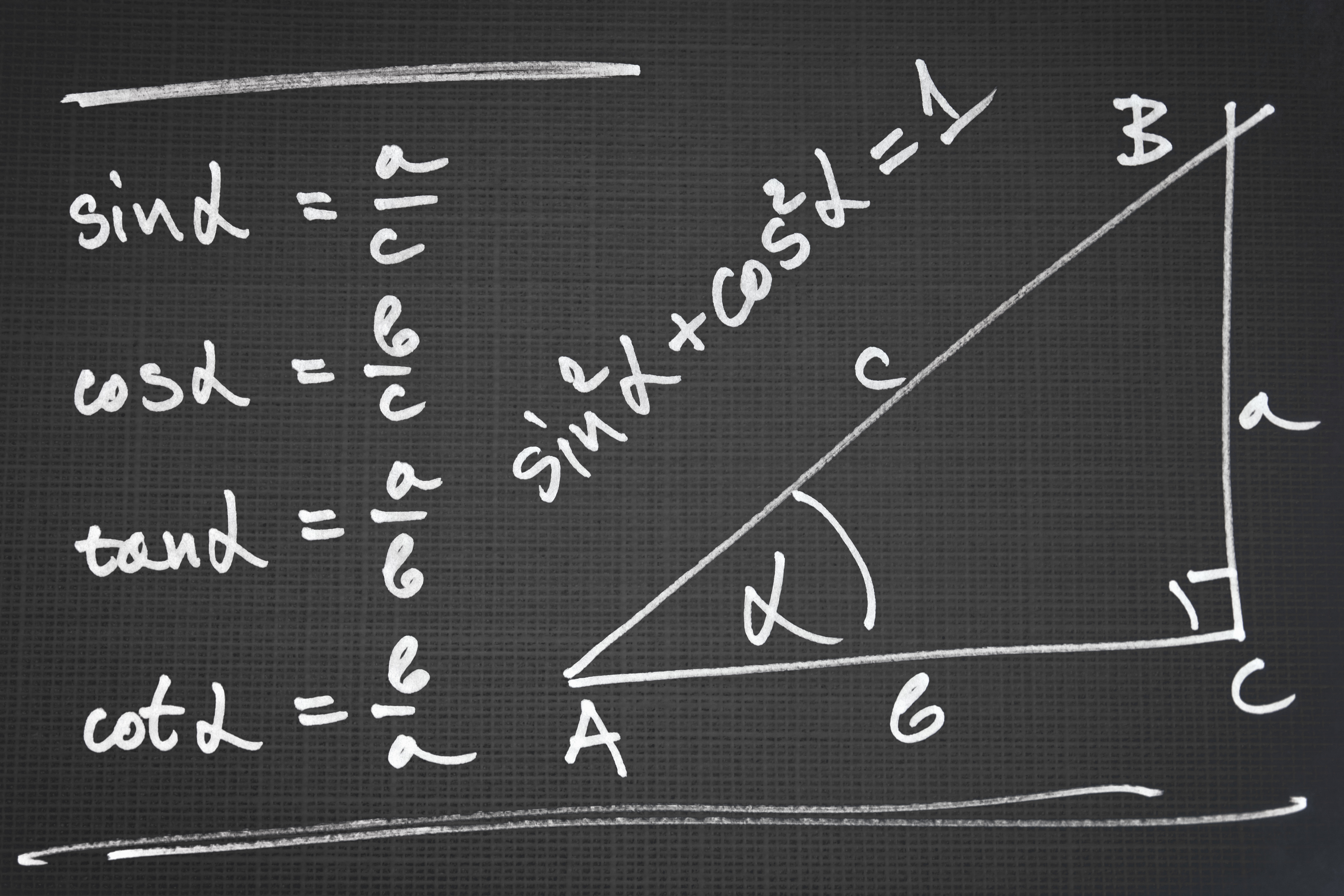


How To Calculate Triangle Quadrilateral Side Lengths


Square Wikipedia



Trigonometry Special Triangles Youtube


Triangle Inequality Wikipedia


Algebra 2 Connections



How To Label Angles In A Right Triangle Tex Latex Stack Exchange



Math Plane Means Extremes And Right Triangles Altitude To Hypotenuse



Right Angle Triangle Trigonometry Review Ck 12 Foundation



3 4 5 Triangle Youtube



Module 13 Trigonometry With Right Triangles Ppt Download



Trig Values Of Special Angles Video Khan Academy
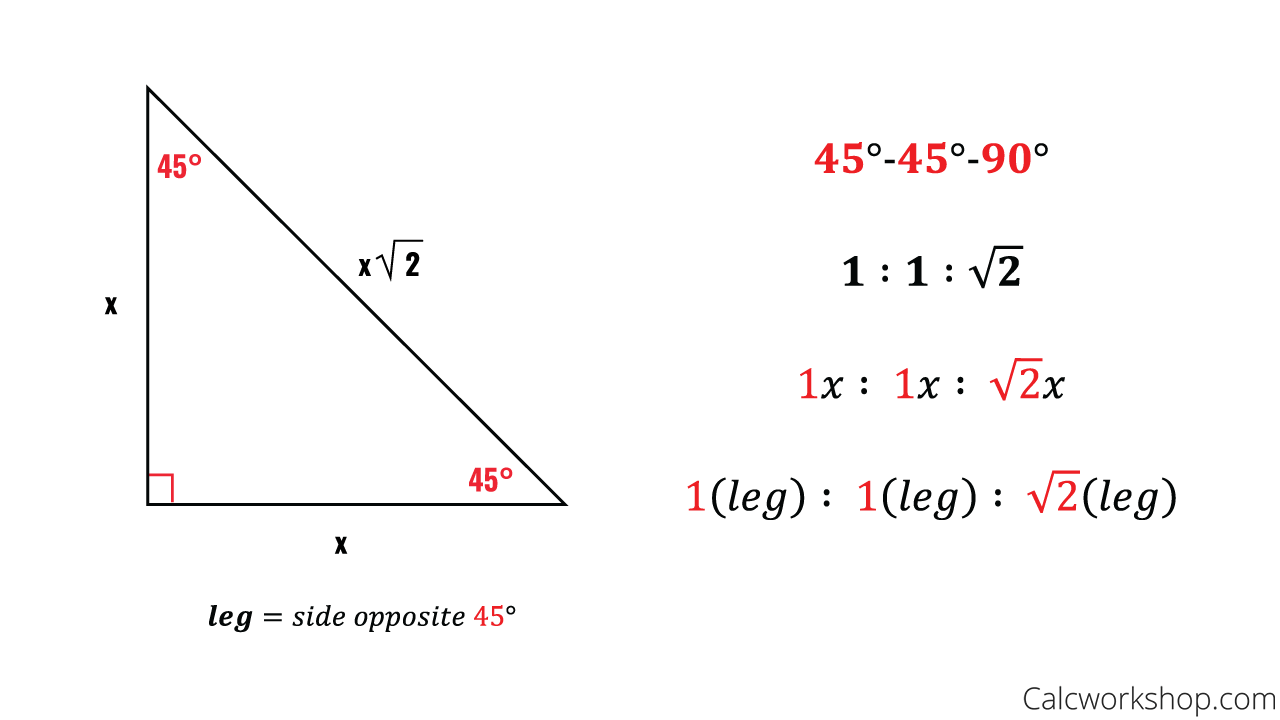


Special Right Triangles Fully Explained W 19 Examples
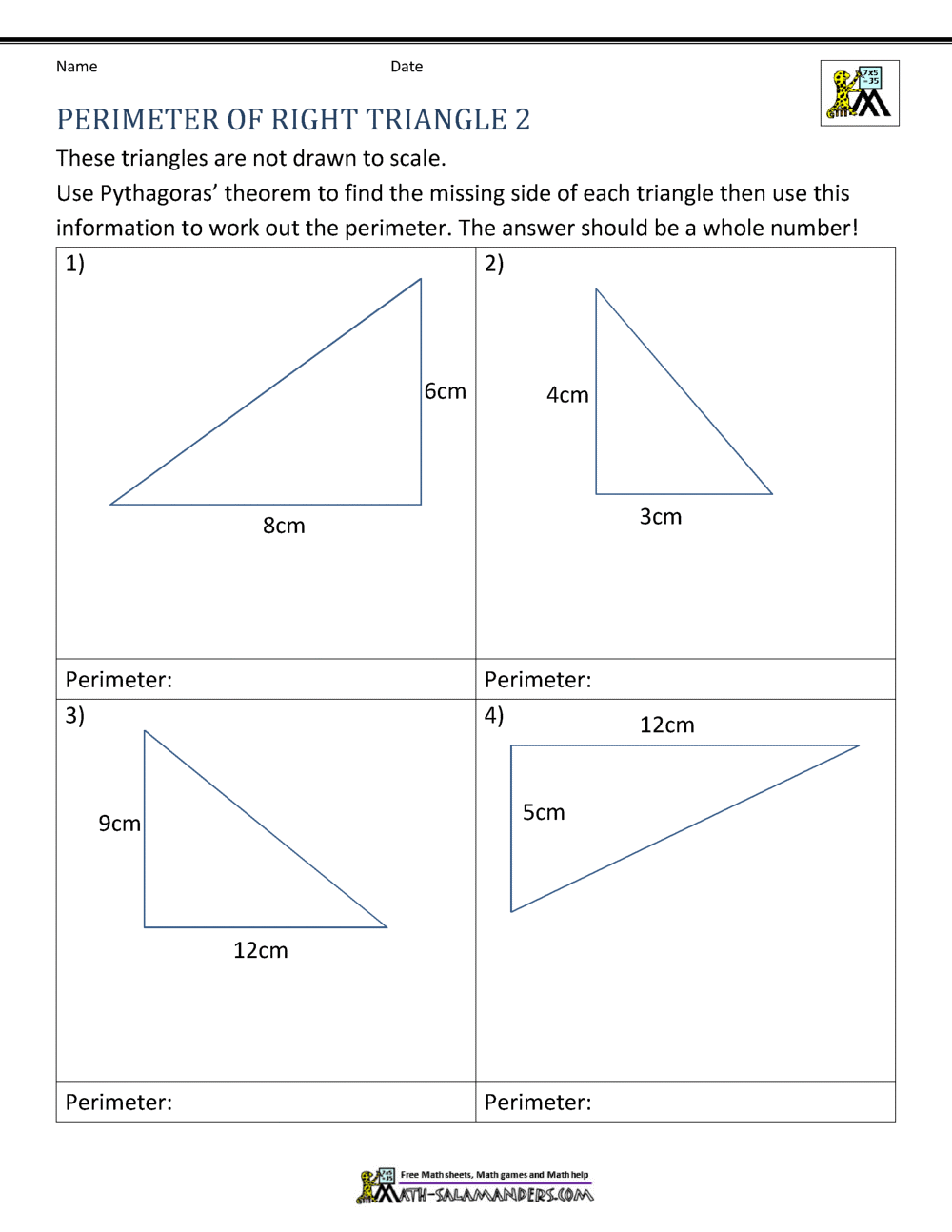


Perimeter Of Right Triangle
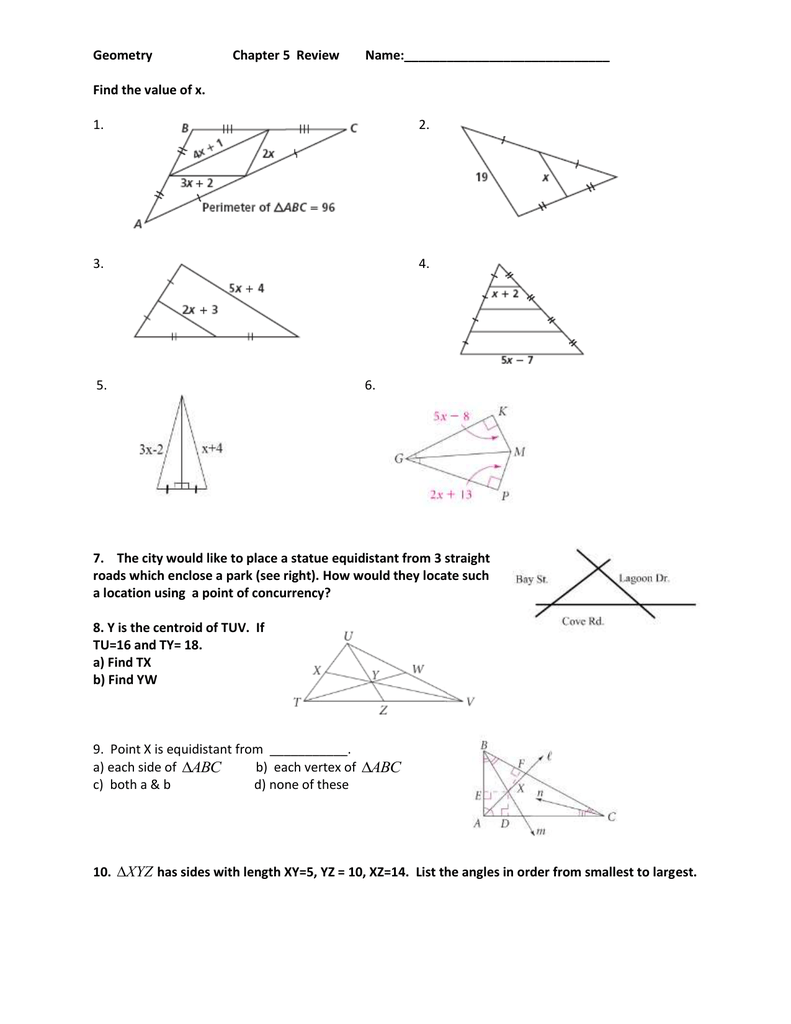


Geometry Chapter 5 Review Find The Value Of X



Finding The Right Angle Thisiscarpentry



How To Calculate Angles 9 Steps With Pictures Wikihow



File Special Right Triangles For Trig Svg Wikimedia Commons



Special Right Triangles Made Easy Youtube



Math Plane Right Triangle Review



Pythagorus Theorum Math Lesson 3 4 5 Triangle Youtube



0 件のコメント:
コメントを投稿